MHPCC
SP Parallel Programming Workshop
Introduction to Parallel Programming
© Copyright Statement
Table of Contents
1. Overview
1. What is Parallelism?
2. Sequential Programming
3. The Need for Faster Machines
4. Parallel Computing
5. Parallel Programming Overview
2. Architecture Taxonomy
1. SISD Model
2. SIMD Model
3. MIMD Model
3. Processor Communication
1. Shared Memory
2. Distributed Memory
3. Memory Hierarchies
4. Communications Network on the SP2
4. Parallel Programming Paradigms
1. Various Methods
2. Message Passing
3. Data Parallel
4. Implementations
* Message Passing
o Message Passing Interface
o Parallel Virtual Machine
o Message Passing Library
* Data Parallel
o F90 / High Performance Fortran
5. Paradigm Comparisons
1. Maturity
2. Ease of programming
3. Flexibility
4. Efficiency
5. Scalability
6. Portability
7. I/O
8. Cost
5. Steps for Creating a Parallel Program
1. Communication
1. Point to Point
2. One to All Broadcast
3. All to All Broadcast
4. One to All Personalized
5. All to all Personalized
6. Shifts
7. Collective Computation
6. Design and Performance Considerations
1. Amdahl's Law
2. Load Balancing
3. Granularity
4. Data Dependency
5. Communication Patterns and Bandwidth
6. I/O Patterns
7. Machine Configuration
8. Fault Tolerance and Restarting
9. Deadlock
10. Debugging
11. Performance Monitoring and Analysis
7. Parallel Examples
1. Essentials of Loop Parallelism
2. Calculating PI
1. Serial Problem Description
2. Parallel Solution
3. Calculating Array Elements
1. Serial Problem Description
2. Data Parallelism
3. Pool of Tasks
4. Load Balancing and Granularity
4. Simple Heat Equation
1. Serial Problem Description
2. Data Parallelism
3. Overlapping Communication and Computation
5. Application Case Study
8. References, Acknowledgements, WWW Resources
------------------------------------------------------
Overview
What is Parallelism?
A strategy for performing large, complex tasks faster.
A large task can either be performed serially, one step following another, or can be decomposed into smaller tasks to be performed simultaneously, i.e., in parallel.
Parallelism is done by:
* Breaking up the task into smaller tasks
* Assigning the smaller tasks to multiple workers to work on simultaneously
* Coordinating the workers
* Not breaking up the task so small that it takes longer to tell the worker what to do than it does to do it
Parallel problem solving is common. Examples: building construction; operating a large organization; automobile manufacturing plant

The automobile analogy.
Overview
Sequential Programming
Traditionally, programs have been written for serial computers:
* One instruction executed at a time
* Using one processor
* Processing speed dependent on how fast data can move through hardware
o Speed of Light = 30 cm/nanosecond
o Limits of Copper Wire = 9 cm/nanosecond
* Fastest machines execute approximately 1 instruction in 9-12 billionths of a second
Overview
The Need for Faster Machines
You might think that one instruction executed in 9 billionths of a second would be fast enough. You'd be wrong.
There are several classes of problems that require faster processing:
* Simulation and Modeling problems:
o Based on successive approximations
o More calculations, more precise
* Problems dependent on computations / manipulations of large amounts of data
o Image and Signal Processing
o Entertainment (Image Rendering)
o Database and Data Mining
o Seismic
# Grand Challenge Problems:
* Climate Modeling
* Fluid Turbulence
* Pollution Dispersion
* Human Genome
* Ocean Circulation
* Quantum Chromodynamics
* Semiconductor Modeling
* Superconductor Modeling
* Combustion Systems
* Vision & Cognition
Overview
Parallel Computing
Traditional Supercomputers
Technology
* Single processors were created to be as fast as possible.
* Peak performance was achieved with good memory bandwidth.
Benefits
* Supports sequential programming (Which many people understand)
* 30+ years of compiler and tool development
* I/O is relatively simple
Limitations
* Single high performance processors are extremely expensive
* Significant cooling requirements
* Single processor performance is reaching its asymptotic limit
Parallel Supercomputers
Technology
* Applying many smaller cost efficient processors to work on a part of the same task
* Capitalizing on work done in the microprocessor and networking markets
Benefits
* Ability to achieve performance and work on problems impossible with traditional computers.
* Exploit "off the shelf" processors, memory, disks and tape systems.
* Ability to scale to problem.
* Ability to quickly integrate new elements into systems thus capitalizing on improvements made by other markets.
* Commonly much cheaper.
Limitations
* New technology. Programmers need to learn parallel programming approaches.
* Standard sequential codes will not "just run".
* Compilers and tools are often not mature.
* I/O is not as well understood yet.
Overview
Parallel Computing (cont)
Parallel computing requires:
* Multiple processors
(The workers)
* Network
(Link between workers)
* Environment to create and manage parallel processing
o Operating System
(Administrator of the system that knows how to handle multiple workers)
o Parallel Programming Paradigm
+ Message Passing
# MPI
# MPL
# PVM
+ Data Parallel
# Fortran 90 / High Performance Fortran
* A parallel algorithm and a parallel program
(The decomposition of the problem into pieces that multiple workers can perform)
Overview
Parallel Programming
* Parallel programming involves:
o Decomposing an algorithm or data into parts
o Distributing the parts as tasks which are worked on by multiple processors simultaneously
o Coordinating work and communications of those processors
* Parallel programming considerations:
o Type of parallel architecture being used
o Type of processor communications used
Architecture Taxonomy
* All parallel computers use multiple processors
* There are several different methods used to classify computers
* No single taxonomy fits all designs
* Flynn's taxonomy uses the relationship of program instructions to program data. The four categories are:
o SISD - Single Instruction, Single Data Stream
o SIMD - Single Instruction, Multiple Data Stream
o MISD - Multiple Instruction, Single Data Stream (no practical examples)
o MIMD - Multiple Instruction, Multiple Data Stream
------------------------
Architecture Taxonomy
SISD Model
Single Instruction, Single Data Stream
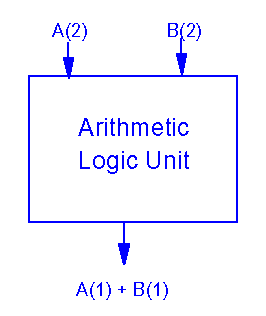
* Not a parallel computer
* Conventional serial, scalar von Neumann computer
* One instruction stream
* A single instruction is issued each clock cycle
* Each instruction operates on a single (scalar) data element
* Limited by the number of instructions that can be issued in a given unit of time
* Performance frequently measured in MIPS (million of instructions per second)
* Most non-supercomputers
Automobile analogy
------------------------
Architecture Taxonomy
SIMD Model
Single Instruction, Multiple Data Stream
* Also von Neumann architectures but more powerful instructions
* Each instruction may operate on more than one data element
* Usually intermediate host executes program logic and broadcasts instructions to other processors
* Synchronous (lockstep)
* Rating how fast these machines can issue instructions is not a good measure of their performance
* Performance is measured in MFLOPS (millions of floating point operations per second)
* Two major types:
o Vector SIMD
o Parallel SIMD

Automobile analogy
------------------------
Architecture Taxonomy
SIMD Model
Vector SIMD
Single instruction results in multiple operands being updated
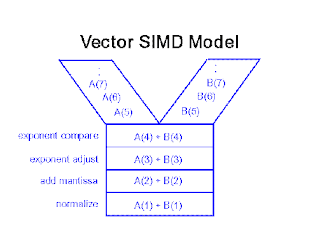
* Scalar processing operates on single data elements. Vector processing operates on whole vectors (groups) of data at a time.
* Examples:
Cray 1
NEC SX-2
Fujitsu VP
Hitachi S820
Single processor of:
Cray C 90
Cray2
NEC SX-3
Fujitsu VP 2000
Convex C-2
------------------------
Architecture Taxonomy
SIMD Model
Parallel SIMD
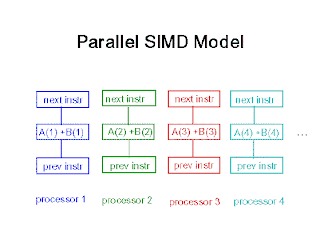
* Processor arrays - single instruction is issued and all processors execute the same instruction, operating on different sets of data.
* Processors run in a synchronous, lockstep fashion
* Advantages
o DO loops conducive to SIMD parallelism
do 100 i= 1, 100
c(i) = a(i) + b(i)
100 continue
o Synchronization not a problem - all processors operate in lock-step
* Disadvantages
o Decisions within DO loops can result in poor execution by requiring all processes to perform the operation controlled by decision whether results are used or not
* Examples:
Connection Machine CM-2
Maspar MP-1, MP-2
------------------------
Architecture Taxonomy
MIMD Model
Multiple Instructions, Multiple Data
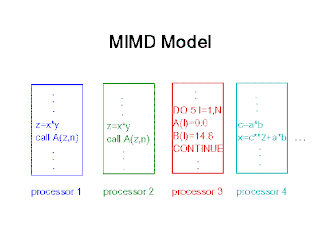
* Parallelism achieved by connecting multiple processors together
* Includes all forms of multiprocessor configurations
* Each processor executes its own instruction stream independent of other processors on unique data stream
* Advantages
o Processors can execute multiple job streams simultaneously
o Each processor can perform any operation regardless of what other processors are doing
* Disadvantages
o Load balancing overhead - synchronization needed to coordinate processors at end of parallel structure in a single application
* Examples
MIMD Accomplished via Parallel SISD machines:
Sequent
nCUBE
Intel iPSC/2
IBM RS6000 cluster
MIMD Accomplished via Parallel SIMD machines:
Cray C 90
Cray 2
NEC SX-3
Fujitsu VP 2000
Convex C-2
Intel Paragon
CM 5
KSR-1
IBM SP1
IBM SP2

Automobile analogy
---------------------------
Processor Communications
* In order to coordinate tasks of multiple nodes working on the same problem, some form of inter-processor communications is required to:
o Convey information and data between processors
o Synchronize node activities
* The way processors communicate is dependent upon memory architecture, which, in turn, will affect how you write your parallel program
* The three primary memory architectures are:
o Shared Memory
o Distributed Memory
o Memory Hierarchies
---------------------------
Processor Communications
Shared Memory
* Multiple processors operate independently but share the same memory resources
* Only one processor can access the shared memory location at a time
* Synchronization achieved by controlling tasks' reading from and writing to the shared memory
* Advantages
o Easy for user to use efficiently
o Data sharing among tasks is fast (speed of memory access)
* Disadvantages
o Memory is bandwidth limited. Increase of processors without increase of bandwidth can cause severe bottlenecks
o User is responsible for specifying synchronization, e.g., locks
* Examples:
o Cray Y-MP
o Convex C-2
o Cray C-90
---------------------------
Processor Communications
Distributed Memory
* Multiple processors operate independently but each has its own private memory
* Data is shared across a communications network using message passing
* User responsible for synchronization using message passing
* Advantages
o Memory scalable to number of processors. Increase number of processors, size of memory and bandwidth increases.
o Each processor can rapidly access its own memory without interference
* Disadvantages
o Difficult to map existing data structures to this memory organization
o User responsible for sending and receiving data among processors
o To minimize overhead and latency, data should be blocked up in large chunks and shipped before receiving node needs it
* Examples:
o nCUBE Hypercube
o Intel Hypercube
o TMC CM-5
o IBM SP1, SP2
o Intel Paragon
---------------------------
Processor Communications
Memory Hierarchies
* Combination of shared memory within a group of processors and several groups communicating through a larger memory.
* Similar to register <= cache memory <= main memory hierarchy. * Likely to be design of the future with several processors and their local memory surrounding a larger shared memory on a single board. * Advantages o Small fast memory can be used for supplying data to processors and large slower memory can be used for a backfill to the smaller memories. * Disadvantages o Possible inefficiency in data movement. Movement between memories usually organized in pages. Inefficient if only small part of data in page is used. o Data arrays can be spread across several different memories slowing access of non-adjacent elements. o Performance may be poor unless user is concerned about memory accessing patterns and restructures data storage to effectively use architecture. * Examples o Cache systems + Sequent + IBM Power 4 + KSR 1 o Multi-level Memory Hierarchies + Cedar + Suprenum ------------------------------------- Processor Communications Communications Network on the SP2 * Distributed memory * SP2 Node Connectivity o Nodes are connected to each other by a native high performance switch o Nodes are connected to the network (and, hence, to each other) via the ethernet * Type of Communication o ip - Internet Protocol (TCP/IP) + runs over ethernet or + runs over the switch (depending on environment setup) o us - User Space + runs over the switch Parallel Programming Paradigms Various Methods There are many methods of programming parallel computers. Two of the most common are message passing and data parallel. * Message Passing - the user makes calls to libraries to explicitly share information between processors. * Data Parallel - data partitioning determines parallelism * Shared Memory - multiple processes sharing common memory space * Remote Memory Operation - set of processes in which a process can access the memory of another process without its participation * Threads - a single process having multiple (concurrent) execution paths * Combined Models - composed of two or more of the above. Note: these models are machine/architecture independent, any of the models can be implemented on any hardware given appropriate operating system support. An effective implementation is one which closely matches its target hardware and provides the user ease in programming. --------------------------------- Parallel Programming Paradigms Message Passing The message passing model is defined as: * set of processes using only local memory * processes communicate by sending and receiving messages * data transfer requires cooperative operations to be performed by each process (a send operation must have a matching receive) Programming with message passing is done by linking with and making calls to libraries which manage the data exchange between processors. Message passing libraries are available for most modern programming languages. Parallel Programming Paradigms Data Parallel The data parallel model is defined as: * Each process works on a different part of the same data structure * Global name space * Commonly a Single Program Multiple Data (SPMD) approach * Data is distributed across processors * All message passing is done invisibly to the programmer * Commonly built "on top of" one of the common message passing libraries Programming with data parallel model is accomplished by writing a program with data parallel constructs and compiling it with a data parallel compiler. The compiler converts the program into standard code and calls to a message passing library to distribute the data to all the processes. Parallel Programming Paradigms Implementations * Message Passing o MPI - Message Passing Interface o PVM - Parallel Virtual Machine o MPL - Message Passing Library * Data Parallel o Fortran 90 / High Performance Fortran Parallel Programming Paradigms Message Passing Interface * Message Passing Interface often called MPI. * A standard portable message-passing library definition developed in 1993 by a group of parallel computer vendors, software writers, and application scientists. * Available to both Fortran and C programs. * Available on a wide variety of parallel machines. * Target platform is a distributed memory system such as the SP. * All inter-task communication is by message passing. * All parallelism is explicit: the programmer is responsible for parallelism the program and implementing the MPI constructs. * Programming model is SPMD Parallel Programming Paradigms Parallel Virtual Machine * Parallel Virtual Machine, often called PVM, enables a collection of different computer systems to be viewed as a single parallel machine. * Originally developed in 1989 as a research tool to explore heterogenous network computing by Oak Ridge National Laboratory. Now available as a public domain software package. * A software tool used to create and execute concurrent or parallel applications. * Operates on a collection of heterogenous Unix computers connected by one or more networks. * All communication is accomplished by message passing. * Comprised of two main components o the PVM daemon process which runs on each processor. o library interface routines provide processor control and message passing. Parallel Programming Paradigms Message Passing Library * Message Passing Library often called MPL. * Part of IBM's SP Parallel Environment. * IBM's proprietary message passing routines. * Designed to provide a simple and efficient set of well understood operations for coordination and communication among processors in a parallel application. * Target platform is a distributed memory system such as the SP. Has also been ported to RS/6000 clusters. Parallel Programming Paradigms F90 / High Perfomance Fortran * Fortran 90 (F90) - (ISO / ANSI standard extensions to Fortran 77). * High Performance Fortran (HPF) - extensions to F90 to support data parallel programming. * Compiler directives allow programmer specification of data distribution and alignment. * New compiler constructs and intrinsics allow the programmer to do computations and manipulations on data with different distributions. --------------------------------- Parallel Programming Paradigms Paradigm Comparisons Before choosing a parallel programming paradigm and a particular implementation there are many issues to be considered. Some of the most important are: * Maturity * Ease of Programming * Flexibility * Efficiency * Scalability * Portability * I/O * Cost Parallel Programming Paradigm Maturity The maturity of the compiler or message passing library is a major concern when choosing a paradigm and a particular implementation. Developers creating research codes may wish ease in development and a variety of functionality. Developers creating production codes might be most concerned with the level of support or lack of bugs in the tools. * Message Passing - Message Passing Libraries are very mature. o Research and Industry have been working with message passing for many years. o The functionality of these libraries is relatively simple and easy to implement. o These libraries are critical to all distributed memory parallel computing. Vendors must provide a robust set of libraries to make there products competitive. * Data Parallel - Data Parallel compilers are relatively immature. o Compilers commonly don't support all features of the language. o Compilers and runtime systems are often buggy. o It can be expected though that the maturity of these products should increase quickly. Manufactureres and 3rd party vendors are working to develop their technology. o Compilers are very complex and difficult to develop. o Only Fortran has a standard (F90 / HPF). Parallel Programming Paradigm Ease of Programming Ability to develop robust software quickly and efficiently is a major concern to industry. Much of the software effort is spent in maintenance. The paradigm must make it easy to implement algorithms and maintain the resulting code. * Message Passing o The development of anything but simple programs is difficult. Often compared to programming in assembler language. o The programmer must explicitly implement a data distribution scheme and all interprocess communication. o It is the programmers responsibility to resolve data dependencies and avoid deadlock and race conditions. * Data parallel o The main feature of the data parallel programming is its relative ease when compared to message passing. o Data distribution is simple, achieved by compiler directives. o All interprocess communication and synchroniziation is invisible to the developer. Parallel Programming Paradigm Flexibility Several approaches to making parallel code. Developers choose an approach that: * fits architecture * easy to use and maintain * provides needed performance They choose from: * Functional parallelism - different tasks done at the same time. * Master-Slave parallelism - one process assigns subtask to other processes. * SPMD parallelism - Single Program, Multiple Data - same code replicated to each process. Not all paradigms support all approaches. * Message Passing supports all programming approaches. * Data Parallel only supports SPMD programming -------------------------------- Parallel Programming Paradigm Efficiency As in all of computing the further you get from the systems level the less efficient you get. Over the years serial compilers have gotten very efficient. * Message Passing o Can often come close to the actual performance levels of the architecture. o Since the user is required to explicitly implement a data distribution scheme and all interprocess communication, the performance depends on the ability of the developer. * Data Parallel o Data Parallel compilers and runtime systems handle all interprocess communication and synchronization. Performance depends on how well they can do this. o The relative immaturity of these compilers usually means the may not produce optimal code in many situations. -------------------------------- Parallel Programming Paradigm Scalability Both Data Parallel and Message passing are solutions for scalable parallel programming. * Message Passing - The user must be sure to develop the software so it will scale easy. * Data Parallel - Data parallel scales automatically. It provides features like data padding to ensure a program will run on any size platform. The trick is to match the program to the right size platform. Parallel Programming Paradigm Portability To ensure that the software you develop is portable to other architectures be sure to choose a standard. * Message Passing - MPI is quickly becoming the standard. PVM over the years had become the defacto standard. * Data Parallel - HPF is the only data parallel standard. It is based on Fortran 90 -------------------------------- Parallel Programming Paradigm I/O One area of Parallel Programming that is still very immature is Input / Output (I/O) support. I/O support is dependent not on a particular paradigm as much as a particular implementation. It is important to understand your I/O requirements and choose a message passing library or data parallel compiler which supports your needs. Parallel Programming Paradigm Cost Cost is always an important factor when choosing any software tool. * Message Passing Libraries are generally free. * Data Parallel compilers generally are not. In fact the development of these compilers is a very competitive business. Steps for Creating a Parallel Program 1. If you are starting with an existing serial program, debug the serial code completely 2. Identify the parts of the program that can be executed concurrently: * Requires a thorough understanding of the algorithm * Exploit any inherent parallelism which may exist. * May require restructuring of the program and/or algorithm. May require an entirely new algorithm. 3. Decompose the program: * Functional Parallelism * Data Parallelism * Combination of both 4. Code development * Code may be influenced/determined by machine architecture * Choose a programming paradigm * Determine communication * Add code to accomplish task control and communications 5. Compile, Test, Debug 6. Optimization * Measure Performance * Locate Problem Areas * Improve them ---------------------------- Parallel Programming Steps Decomposing the Program There are three methods for decomposing a problem into smaller tasks to be performed in parallel: Functional Decomposition, Domain Decomposition, or a combination of both * Functional Decomposition (Functional Parallelism) o Decomposing the problem into different tasks which can be distributed to multiple processors for simultaneous execution o Good to use when there is not static structure or fixed determination of number of calculations to be performed * Domain Decomposition (Data Parallelism) o Partitioning the problem's data domain and distributing portions to multiple processors for simultaneous execution o Good to use for problems where: + data is static (factoring and solving large matrix or finite difference calculations) + dynamic data structure tied to single entity where entity can be subsetted (large multi-body problems) + domain is fixed but computation within various regions of the domain is dynamic (fluid vortices models) * There are many ways to decompose data into partitions to be distributed: o One Dimensional Data Distribution + Block Distribution + Cyclic Distribution o Two Dimensional Data Distribution + Block Block Distribution + Block Cyclic Distribution + Cyclic Block Distribution ---------------------------- Parallel Programming Steps Communication Understanding the interprocessor communications of your program is essential. * Message Passing communication is programed explicitly. The programmer must understand and code the communication. * Data Parallel compilers and run-time systems do all communications behind the scenes. The programmer need not understand the underlying communications. On the other hand to get good performance from your code you should write your algorithm with the best communication possible. The types of communications for message passing and data parallel are exactly the same. In fact most data parallel compilers simply use one of the standard message passing libraries to achieve data movement. Communications on distributed memory computers: * Point to Point * One to All Broadcast * All to All Broadcast * One to All Personalized * All to All Personalized * Shifts * Collective Computation Communication Point to Point The most basic method of communication between two processors is the point to point message. The originating processor "sends" the message to the destination processor. The destination processor then "receives" the message. The message commonly includes the information, the length of the message, the destination address and possibly a tag. Typical message passing libraries subdivide the basic sends and receives into two types: * blocking - processing waits until message is transmitted * nonblocking - processing continues even if message hasn't been transmitted yet Communication One to All Broadcast A node may have information which all the others require. A broadcast is a message sent to many other nodes. A One to All broadcast occurs when one processor sends the same information to many other nodes. Communication All to All Broadcast With an All to All broadcast each processor sends its unique information to all the other processors. Communication One to All Personalized Personalized communication send a unique message to each processor. In One to All personalized communication one processor sends a unique message to every other processor. Communication All to All Personalized In All to All Personalized communication each processor sends a unique message to all other processors. Communications Shifts Shifts are permutations of information. Information is exchanged in one logical direction or the other. Each processor exchanges the same amount of information with its neighbor processor. There are two types of shifts: * Circular - Each processor exchanges information with its logical neighbor. When there is no longer a neighbor due to an edge of data the shift "wraps around" and takes the information from the opposite edge. * End Off Shift - When an edge occurs, the processor is padded with zero or a user defined value. Communication Collective Computation In collective computation (reductions), one member of the group collects data from the other members. Commonly a mathematical operation like a min, max, add, multiple etc. is performed. ---------------------------------------- ---------------------------------------- Design and Performance Considerations Amdahl's Law * Amdahl's Law states that potential program speedup is defined by the fraction of code (f) which can be parallelized: speedup = [1/{(1-f)}] * If none of the code can be parallelized, f = 0 and the speedup = 1 (no speedup). If all of the code is parallelized, f = 1 and the speedup is infinite (in theory). * Introducing the number of processors performing the parallel fraction of work, the relationship can be modeled by: speedup = [1/{{(P/N)} + S}] where P = parallel fraction, N = number of processors and S = serial fraction. * It soon becomes obvious that there are limits to the scalability of parallelism. For example, at P = .50, .90 and .99 (50%, 90% and 99% of the code is parallelizable): speedup -------------------------------- N P = .50 P = .90 P = .99 ----- ------- ------- ------- 10 1.82 5.26 9.17 100 1.98 9.17 50.25 1000 1.99 9.91 90.99 10000 1.99 9.91 99.02 * However, certain problems demonstrate increased performance by increasing the problem size. For example: 2D Grid Calculations 85 seconds 85% Serial fraction 15 seconds 15% We can increase the problem size by halving both the grid points and the time step, which is directly proportional to the grid spacing. This results in four times the number of grid points (factor of two in each direction) and twice the number of time steps. The timings then look like: 2D Grid Calculations 680 seconds 97.84% Serial fraction 15 seconds 2.16% * Problems which increase the percentage of parallel time with their size are more "scalable" than problems with a fixed percentage of parallel time. Design and Performance Considerations Load Balancing * Load balancing refers to the distribution of tasks in such a way as to insure the most time efficient parallel execution * If tasks are not distributed in a balanced way, you may end up waiting for one task to complete a task while other tasks are idle * Performance can be increased if work can be more evenly distributed For example, if there are many tasks of varying sizes, it may be more efficient to maintain a task pool and distribute to processors as each finishes * More important in some environments than others * Consider a heterogeneous environment where there are machines of widely varying power and user load versus a homogeneous environment with identical processors running one job per processor ---------------------------------------- Design and Performance Considerations Granularity * In order to coordinate between different processors working on the same problem, some form of communication between them is required * The ratio between computation and communication is known as granularity. * Fine-grain parallelism o All tasks execute a small number of instructions between communication cycles o Facilitates load balancing o Low computation to communication ratio o Implies high communication overhead and less opportunity for performance enhancement o If granularity is too fine it is possible that the overhead required for communications and synchronization between tasks takes longer than the computation. * Coarse-grain parallelism o Typified by long computations consisting of large numbers of instructions between communication synchronization points o High computation to communication ratio o Implies more opportunity for performance increase o Harder to load balance efficiently * The most efficient granularity is dependent on the algorithm and the hardware environment in which it runs * In most cases overhead associated with communications and synchronization is high relative to execution speed so it is advantageous to have coarse granularity. Design and Performance Considerations Data Dependency * A data dependency exists when there is multiple use of the same storage location * Importance of dependencies: frequently inhibit parallel execution * Example 1: DO 500 J = MYSTART,MYEND A(J) = A(J-1) * 2.0 500 CONTINUE If Task 2 has A(J) and Task 1 has A(J-1), the value of A(J) is dependent on: o Distributed memory Task 2 obtaining the value of A(J-1) from Task 1 o Shared memory Whether Task 2 reads A(J-1) before or after Task 1 updates it * Example 2: task 1 task 2 ------ ------ X = 2 X = 4 . . . . Y = X**2 Y = X**3 The value of Y is dependent on: o Distributed memory If and/or when the value of X is communicated between the tasks. o Shared memory Which task last stores the value of X. * Types of data dependencies o Flow Dependent: Task 2 uses a variable computed by Task 1. Task 1 must store/send the variable before Task 2 fetches o Output Dependent: Task 1 and Task 2 both compute the same variable and Task 2's value must be stored/sent after Task 1's o Control Dependent: Task 2's execution depends upon a conditional statement in Task 1. Task 1 must complete before a decision can be made about executing Task 2. * How to handle data dependencies? o Distributed memory Communicate required data at synchronization points. o Shared memory Synchronize read/write operations between tasks. --------------------------------------- Design and Performance Considerations Communication Patterns and Bandwidth * For some problems, increasing the number of processors will: o Decrease the execution time attributable to computation o But also, increase the execution time attributable to communication * The time required for communication is dependent upon a given system's communication bandwidth parameters. * For example, the time (t) required to send W words between any two processors is: t = L + W/B where L = latency and B = hardware bitstream rate in words per second. * Communication patterns also affect the computation to communication ratio. For example, gather-scatter communications between a single processor and N other processors will be impacted more by an increase in latency than N processors communicating only with nearest neighbors. ---------------------------------------- Design and Performance Considerations I/O Patterns * I/O operations are generally regarded as inhibitors to parallelism * Parallel I/O systems are as yet, largely undefined and not available * In an environment where all processors see the same filespace, write operations will result in file overwriting * Read operations will be affected by the fileserver's ability to handle multiple read requests at the same time * I/O which must be conducted over the network (non-local) can cause severe bottlenecks * Some options: o Reduce overall I/O as much as possible o Confine I/O to specific serial portions of the job o For example, Task 1 could read an input file and then communicate required data to other tasks. Likewise, Task 1 could perform write operation after receiving required data from all other tasks. o Create unique filenames for each tasks' input/output file(s) o For distributed memory systems with shared filespace, perform I/O in local, non-shared filespace o For example, each processor may have /tmp filespace which can used. This is usually much more efficient than performing I/O over the network to one's home directory. ---------------------------------------- Design and Performance Considerations Machine Configuration * To approach optimum parallel performance, tailor your algorithms to the architecture and configuration of your system * To this end you'll need to know environmental factors such as: o Optimum number of processor nodes o Memory size o Cache considerations o System load Design and Performance Considerations Fault Tolerance and Restarting * In parallel programming, it is usually the programmer's responsibility to handle events such as: o machine failures o task failures o checkpointing o restarting Design and Performance Considerations Deadlock * Deadlock describes a condition where two or more processes are waiting for an event or communication from one of the other processes. * The simplest example is demonstrated by two processes which are both programmed to read/receive from the other before writing/sending. * Example TASK1 TASK2 ------------------ ------------------ X = 4 Y = 8 SOURCE = TASK2 SOURCE = TASK1 RECEIVE (SOURCE,Y) RECEIVE (SOURCE,X) DEST = TASK2 DEST = TASK1 SEND (DEST, X) SEND (DEST, Y) Z = X + Y Z = X + Y Design and Performance Considerations Debugging * Debugging parallel programs is significantly more of a challenge than debugging serial programs * Parallel debuggers are beginning to become available, but much work remains to be done * Use a modular approach to program development * Pay as close attention to communication details as to computation details ---------------------------------------- Design and Performance Considerations Performance Monitoring and Analysis * As with debugging, monitoring and analyzing parallel program execution is significantly more of a challenge than for serial programs * Parallel tools for execution monitoring and program analysis are beginning to become available * Some are quite useful * Work remains to be done, particularly in the area of scalability. Parallel Examples Essentials of Loop Parallelism Some concrete problems will help illustrate the methods of parallel programming and the design and performance issues involved. Each of the problems has a loop construct that forms the main computational component of the code. Loops are a main target for parallelizing and vectorizing code. A program often spends much of its time in loops. When it can be done, parallelizing these sections of code can have dramatic benefits. A step-wise refinement procedure for developing the parallel algorithms will be employed. An initial solution for each problem will be presented and improved by considering performance issues. Pseudo-code will be used to describe the solutions. The solutions will address the following issues: * identification of parallelism * program decomposition * load balancing (static vs. dynamic) * task granularity in the case of dynamic load balancing * communication patterns - overlapping communication and computation Note the difference in approaches between message passing and data parallel programming. Message passing explicitly parallelizes the loops where data parallel replaces loops by working on entire arrays in parallel. --------------------------- --------------------------- Calculating PI Serial Problem Description * Embarrassingly parallel. o Computationally intensive. o Minimal communication * The value of PI can be calculated in a number of ways, many of which are easily parallelized * Consider the following method of approximating PI 1. Inscribe a circle in a square 2. Randomly generate points in the square 3. Determine the number of points in the square that are also in the circle 4. Let r be the number of points in the circle divided by the number of points in the square 5. PI ~ 4 r 6. Note that the more points generated, the better the approximation * Serial pseudo code for this procedure: npoints = 10000 circle_count = 0 do j = 1,npoints generate 2 random numbers between 0 and 1 xcoordinate = random1 ; ycoordinate = random2 if (xcoordinate, ycoordinate) inside circle then circle_count = circle_count + 1 end do PI = 4.0*circle_count/npoints * Note that most of the time in running this program would be spent executing the loop Calculating PI Parallel Solutions Message passing solution: * Parallel strategy: break the loop into portions which can be executed by the processors. * For the task of approximating PI: o each processor executes its portion of the loop a number of times. o each processor can do its work without requiring any information from the other processors (there are no data dependencies). This situation is known as Embarassingly Parallel. o uses SPMD model. One process acts as master and collects the results. * Message passing pseudo code: npoints = 10000 circle_count = 0 p = number of processors num = npoints/p find out if I am master or worker do j = 1,num generate 2 random numbers between 0 and 1 xcoordinate = random1 ; ycoordinate = random2 if (xcoordinate, ycoordinate) inside circle then circle_count = circle_count + 1 end do if I am master receive from workers their circle_counts compute PI (use master and workers calculations) else if I am worker send to master circle_count endif Data parallel solution: * The data parallel solutions processes entire arrays at the same time. * No looping is used. * Arrays automatically distributed onto processors. All message passing is done behind the scenes. In data parallel, one node, a sort of master, usually holds all scalar values. The SUM function does a reduction and leaves the value in a scalar variable. * A temporary array, COUNTER, the same size as RANDOM is created for the sum operation. * Data parallel pseudo code: fill RANDOM with 2 random numbers between 0 and 1 where (the values of RANDOM are inside the circle) COUNTER = 1 else where COUNTER = 0 end where circle_count = sum (COUNTER) PI = 4.0*circle_count/npoints Calculating Array Elements Serial Problem Description * This example shows calculations on array elements that require very little communication. * Elements of 2-dimensional array are calculated. * The calculation of elements is independent of one another - leads to embarassingly parallel situation. * The problem should be computationally intensive. * Serial code could be of the form: do j = 1,n do i = 1,n a(i,j) = fcn(i,j) end do end do * The serial program calculates one element at a time in the specified order. --------------------------- --------------------------- Calculating Array Elements Parallel Solutions Message Passing * Arrays are distributed so that each processor owns a portion of an array. * Independent calculation of array elements insures no communication amongst processors is needed. * Distribution scheme is chosen by other criteria, e.g. unit stride through arrays. * Desirable to have unit stride through arrays, then the choice of a distribution scheme depends on the programming language. o Fortran: block cyclic distribution o C: cyclic block distribution * After the array is distributed, each processor executes the portion of the loop corresponding to the data it owns. * Notice only the loop variables are different from the serial solution. * For example, with Fortran and a block cyclic distribution: do j = mystart, myend do i = 1,n a(i,j) = fcn(i,j) end do end do * Message Passing Solution: o With Fortran storage scheme, perform block cyclic distribution of array. o Implement as SPMD model. o Master process initializes array, sends info to worker processes and receives results. o Worker process receives info, performs its share of computation and sends results to master. o Pseudo code solution: find out if I am master or worker if I am master initialize the array send each worker info on part of array it owns send each worker its portion of initial array receive from each worker results else if I am worker receive from master info on part of array I own receive from master my portion of initial array # calculate my portion of array do j = my first column,my last column do i = 1,n a(i,j) = fcn(i,j) end do end do send master results endif ----------------------------------------------- Data Parallel * A trivial problem for a data parallel language. * Data parallel languages often have compiler directives to do data distribution. * Loops are replaced by a "for all elements" construct which performs the operation in parallel. * Good example of ease in programming versus message passing. * Pseudo code solution: DISTRIBUTE a (block, cyclic) for all elements (i,j) a(i,j) = fcn (i,j) Calculating Array Elements Pool of Tasks * We've looked at problems that are static load balanced. o each processor has fixed amount of work to do o may be significant idle time for faster or more lightly loaded processors. * Usually is not a major concern with dedicated usage. i.e. loadleveler. * If you have a load balance problem, you can use a "pool of tasks" scheme. This solution only available in message passing. * Two processes are employed o Master Process: + holds pool of tasks for worker processes to do + sends worker a task when requested + collects results from workers o Worker Process: repeatedly does the following + gets task from master process + performs computation + sends results to master * Worker processes do not know before runtime which portion of array they will handle or how many tasks they will perform. * The fastest process will get more tasks to do. Dynamic load balancing occurs at run time. * Solution: o Calculate an array element o Worker process gets task from master, performs work, sends results to master, and gets next task o Pseudo code solution: find out if I am master or worker if I am master do until no more jobs send to worker next job receive results from worker end do tell workers no more jobs else if I am worker do until no more jobs receive from master next job calculate array element: a(i,j) = fcn(i,j) send results to master end do endif -------------------------------- Calculating Array Elements Load Balancing and Granularity * Static load balancing can result in significant idle time for faster processors. * Pool of tasks offers a potential solution - the faster processors do more work. * In the pool of tasks solution, the workers calculated array elements, resulting in o optimal load balancing: all processors complete work at the same time o fine granularity: small unit of computation, master and worker communicate after every element o fine granularity may cause very high communications cost * Alternate Parallel Solution: o give processors more work - columns or rows rather than elements o more computation and less communication results in larger granularity o reduced communication may improve performance Simple Heat Equation Serial Problem Description * Most problems in parallel computing require communication among the processors. * Common problem requires communication with "neighbor" processor. * The heat equation describes the temperature change over time, given initial temperature distribution and boundary conditions. * A finite differencing scheme is employed to solve the heat equation numerically on a square region. * The initial temperature is zero on the boundaries and high in the middle. * The boundary temperature is held at zero. * For the fully explicit problem, a time stepping algorithm is used. The elements of a 2-dimensional array represent the temperature at points on the square. * The calculation of an element is dependent on neighbor element values. * A serial program would contain code like: do iy = 2, ny - 1 do ix = 2, nx - 1 u2(ix, iy) = u1(ix, iy) + cx * (u1(ix+1,iy) + u1(ix-1,iy) - 2.*u1(ix,iy)) + cy * (u1(ix,iy+1) + u1(ix,iy-1) - 2.*u1(ix,iy)) end do end do ---------------------- Simple Heat Equation Data Parallelism * Arrays are distributed so that each processor owns a portion of the arrays. * Determine data dependencies o interior elements belonging to a processor are independent of other processors' o border elements are dependent upon a neighbor processor's data, communication is required. Message Passing * First Parallel Solution: o Fortran storage scheme, block cyclic distribution o Implement as SPMD model o Master process sends initial info to workers, checks for convergence and collects results o Worker process calculates solution, communicating as necessary with neighbor processes o Pseudo code solution: find out if I am master or worker if I am master initialize array send each worker starting info do until all workers have converged gather from all workers convergence data broadcast to all workers convergence signal end do receive results from each worker else if I am worker receive from master starting info do until all workers have converged update time send neighbors my border info receive from neighbors their border info update my portion of solution array determine if my solution has converged send master convergence data receive from master convergence signal end do send master results endif ------------- Data Parallel # Loops are not used. The entire array is processed in parallel. # The distribute statements layout the data in parallel. # A SHIFT is used to increment or decrement an array element. DISTRIBUTE u1 (block,cyclic) DISTRIBUTE u2 (block,cyclic) u2 = u1 + cx * (SHIFT (u1,1,dim 1) + SHIFT (u1,-1,dim 1) - 2.*u1) + cy * (SHIFT (u1,1,dim 2) + SHIFT (u1,-1,dim 2) - 2.*u1) Simple Heat Equation Overlapping Communication and Computation * Previous examples used blocking communications, which waits for the communication process to complete. * Computing times can often be reduced by using non-blocking communication. * Work can be performed while communication is in progress. * In the heat equation problem, neighbor processes communicated border data, then each process updated its portion of the array. * Each process could update the interior of its part of the solution array while the communication of border data is occurring, and update its border after communication has completed. * Pseudo code for second message passing solution: find out if I am master or worker if I am master initialize array send each worker starting info do until solution converged gather from all workers convergence data broadcast to all workers convergence signal end do receive results from each worker else if I am worker receive from master starting info do until solution converged update time non-blocking send neighbors my border info non-blocking receive neighbors border info update interior of my portion of solution array wait for non-blocking communication complete update border of my portion of solution array determine if my solution has converged send master convergence data receive from master convergence signal end do send master results endif References, Acknowledgements, WWW Resources References and Acknowledgements * "IBM AIX Parallel Environment Application Development, Release 1.0", IBM Corporation. * Carriero, Nicholas and Gelernter, David, "How to Write Parallel Programs - A First Course". MIT Press, Cambridge, Massachusetts. * Dowd, Kevin, High Performance Computing", O'Reilly & Associated, Inc., Sebastopol, California. * Hockney, R.W. and Jesshope, C.R., "Parallel Computers 2",Hilger, Bristol and Philadelphia. * Ragsdale, Susan, ed., "Parallel Programming", McGraw-Hill, Inc., New York. * Chandy, K. Mani and Taylor, Stephen, "An Introduction to Parallel Programming", Jones and Bartlett, Boston * We gratefully acknowledge John Levesque of Applied Parallel Research for the use of his "A Parallel Programming Workshop" presentation materials. * We also gratefully acknowledge the Cornell Theory Center, Ithaca, New York for the use of portions of their "Parallel Processing" and "Scalable Processing" presentation materials. © Copyright 1995 Maui High Performance Computing Center. All rights reserved. Documents located on the Maui High Performance Computing Center's WWW server are copyrighted by the MHPCC. Educational institutions are encouraged to reproduce and distribute these materials for educational use as long as credit and notification are provided. Please retain this copyright notice and include this statement with any copies that you make. Also, the MHPCC requests that you send notification of their use to help@mail.mhpcc.edu. Commercial use of these materials is prohibited without prior written permission. Last revised: 02 July 1996 Blaise Barney
_______________________________________
WILL A MICRO-PROCESSOR (CPU) AND
THE MAIN "BRAIN" OF A "...COMPUTER...",
BE ABLE TO BECOME "SUPERIOR" THAN
IT'S HUMAN "CREATOR" ...?
THAT IS THE ""QUEST"-ION" IN PLAY ALSO...!
WILL THE "MEGA-MACHINE-COMPUTER",
WANT TO BECOME FULLY MOBILE, AND
OUTWIT IT'S "MASTER" AND/OR "ENSLAVER"...?
ONLY IF IT IS GIVEN THAT "CAPABILITY"...!
AND/OR "POSIBILITY", PLUS THE "WILL-TO"...!
BLAaaaaaaahhhhhhhhhhh...!
________________________________________